背包问题

背包九讲

0-1背包

题目

有$N$件物品和最多承载量$W$的背包。第$i$件物品的重量是$w_i$，其价值是$v_i$。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

基本思路

作为最基础的背包问题，其特点是每件物品最多用一次
用子问题定义状态$F[i,w]$表示前$i$件物品放入承载量$w$的背包可获得的最大价值，则状态转移方程便是

$$F[i,w] = max(F[i-1,w],F[i-1,w-w_i]+v_i)$$

其代表的意思是若只考虑第$i$件物品的策略（放或不放），那么就可以转化为一个只和前$i-1$件物品相关的问题。

• 如果不放第$i$件物品，问题就转化为“前$i-1$件物品放入容量为$w$的背包中”，价值为$F[i-1,w]$；
• 如果放第$i$件物品，问题就转化为“前$i-1$件物品放入剩下的容量为$w-w_i$的背包中”，此时能获得的最大价值就是$F[i-1,w-w_i]$再加上通过放入第i件物品获得的价值 $w_i$。

代码实现

先遍历物品再遍历容量(横向更新)

先遍历容量再遍历物品(纵向更新)

蓝色方块表示更新完成，绿色表示当前需要更新的值，红色表示还未更新，带文字的方块表示更新当前值所需要的值。
可以看出，对于二维实现，先遍历背包容量或者先遍历物品都可以，因为更新当前位置所需信息时所需要的值(蓝色带文字方块)都已经更新完成

$bagWeight$为背包重量，$weight$表示重量数组，$value$表示价值数组，

//先遍历物品再遍历容量(横向更新)      
int zeroOnePack(int bagWeight,vector<int> weight,vector<int> value){
    int m = weight.size(), n = bagWeight;
    // dp[i][j] 表示对于前i件物品，容量为j的背包所能获得的最大价值
    //初始化 dp[*][0] = 0 dp[0][*] = 0
    int dp[m+1][n+1];
    for(int i = 0; i < m+1; i++)
        dp[i][0] = 0;
    for(int i = 0; i < n+1; i++)
        dp[0][i] = 0;

    for(int i = 1; i < weight.size(); i++) { // 遍历物品
        for(int j = 1; j <= bagWeight; j++) { // 遍历背包容量
            if (j < weight[i]) 
                dp[i][j] = dp[i - 1][j]; 
            else 
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
        }
    }
    return dp[m][n];
}

//先遍历容量再遍历物品(纵向更新)
for(int j = 1; j <= bagWeight; j++) { // 遍历背包容量
    for(int i = 1; i < weight.size(); i++) { // 遍历物品
        if (j < weight[i]) 
            dp[i][j] = dp[i - 1][j];
        else 
            dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
    }
}

空间优化

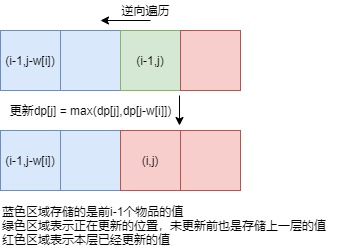
采用一维数组去替代二维数组，这要求在dp能够同时保存上一层信息和更新本层
因为更新当前位置所需信息只在上一层左边和正上方，必需采用逆序。

int zeroOnePack(int bagWeight,vector<int> weight,vector<int> value){
    vector<int> dp(bagWeight+1,0);
    for(int i = 0; i < weight.size(); i++) { // 遍历物品

        
        for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
            //这样保证物体i只在本次循环被使用，因为等式右边的dp保存的是前i-1个物品
            dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
        }
    }
    return dp[bagWeight];   

}

完全背包

完全背包与0-1背包的区别在于物品的个数是无限的，即可重复选择相同物品填充

基本思路

1. 基本思路
   模仿0-1背包的解法

$$F[i,w] = max\{F[i-1,w-k*w_i]+k*v_i | 0<=k*w_i<=W\}$$

2. 转换为0-1背包
   每个物品i,最多能放$\frac{W}{w_i}$件，那么就把第$i$件扩充至$\frac{W}{w_i}$件，然后解决这个0-1背包问题
   则状态转移方程便是

   $$F[i,w] = max(F[i-1,w],F[i,w-w_i]+v_i)$$

• 如果不放第$i$件物品，问题就转化为“前$i-1$件物品放入容量为$w$的背包中”，价值为$F[i-1,w]$；
• 在考虑“选一件第$i$种物品”时，需要一个可能已选入第$i$种物品的子结果$F[i,w-w_i]$。而不是只选到前$i-1$的子结果$F[i-1,w-w_i]$

二维实现

先遍历物品再遍历容量(横向更新)

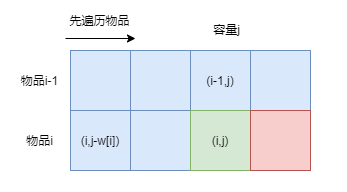
先遍历容量再遍历物品(纵向更新)

和0-1背包一样，对于二维实现，先遍历物品和先遍历容量都是可行的。原因就在于不管采用那种遍历顺利总是保证更新当前位置时所需要的信息已经准备好了

$bagWeight$为背包重量，$weight$表示重量数组，$value$表示价值数组，

int completePack(int bagWeight,vector<int> weight,vector<int> value){
    int m = weight.size(), n = bagWeight;
    // dp[i][j] 表示对于前i件物品，容量为j的背包所能获得的最大价值
    //初始化 dp[*][0] = 0 dp[0][*] = 0
    int dp[m+1][n+1];
    for(int i = 0; i < m+1; i++)
        dp[i][0] = 0;
    for(int i = 0; i < n+1; i++)
        dp[0][i] = 0;

    for(int i = 1; i < weight.size(); i++) { // 遍历物品
        for(int j = 1; j <= bagWeight; j++) { // 遍历背包容量
            if (j < weight[i]) 
                dp[i][j] = dp[i - 1][j]; 
            else 
                dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]);
        }
    }
    return dp[m][n];
}

空间优化

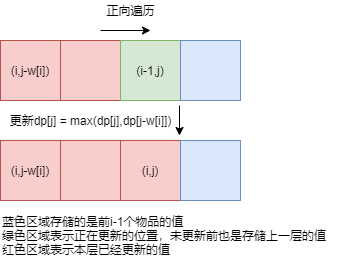
采用一维数组去替代二维数组，
因为更新当前位置所需信息本层左边和正上方，对应到一维就是当前位置左边和自身位置，需采用正向遍历，及时更新本层左边方块

int completePack(int bagWeight,vector<int> weight,vector<int> value){
    vector<int> dp(bagWeight+1,0);
    for(int i = 0; i < weight.size(); i++) { // 遍历物品       
        for(int j = weight[i]; j <= bagWeight; j++) { // 遍历背包容量
            dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
        }
    }
    return dp[bagWeight];   
}

总结

1. 不管是0-1背包还是完全背包，其二维实现两种遍历顺序都是可以的
2. 0-1背包和完全背包解决的是组合问题，并非排列问题，排列问题参考爬楼梯
3. 0-1背包和完全背包组合问题都是外层遍历物品，内层遍历背包容量。
4. 0-1背包是逆向遍历背包容量，保证当前物品最多一个被加入。完全背包正向遍历，使得可以当前物品可多次被加入
5. 对于排列问题，先遍历背包，在遍历物品。参考爬楼梯进阶版