排序算法(三)——堆、计数、桶、基数排序

堆排序

堆排序(Heapsort)是指利用堆积树（堆）这种数据结构所设计的一种排序算法，它是选择排序的一种。可以利用数组的特点快速定位指定索引的元素。堆排序就是把最大堆堆顶的最大数取出，将剩余的堆继续调整为最大堆，再次将堆顶的最大数取出，这个过程持续到剩余数只有一个时结束。

堆的概念

堆是一种完全二叉树，这使得堆(完全二叉树)可以用数组进行表示。如下图每一个节点对应数组的一个元素且可以通过数组下标来判断节点间位置。
对于给定下标为i的数组中的数组,其该元素所对应的父节点、孩子节点下标为(以1作为开始)：
父节点： Parent(i) = floor(i/2)
左孩子节点： Left(i) = 2*i
右孩子节点: Right(i)= 2*i +1

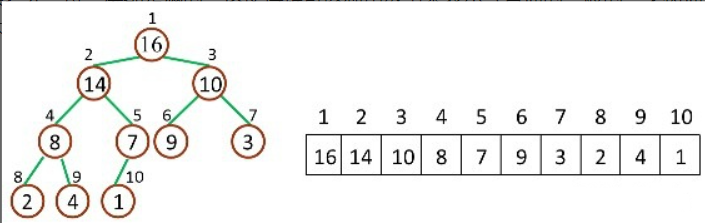
• 最大堆即最大元素值出现在根结点，堆中每个父节点的元素值都大于等于其孩子结点 用于升序排列
• 最小堆中的最小元素值出现在根结点，堆中每个父节点的元素值都小于等于其孩子结点 用于降序排列

算法描述

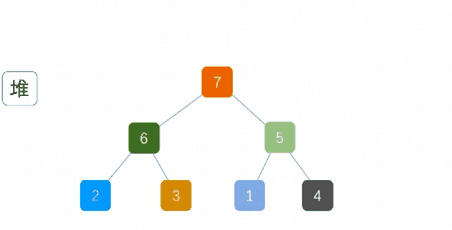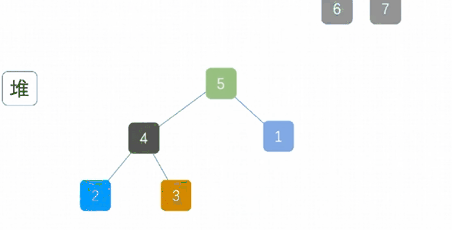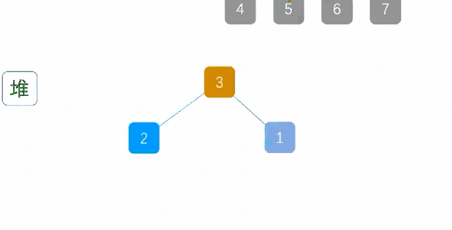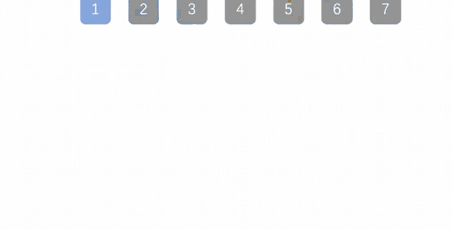
堆排序就是把最大堆堆顶的最大数取出，将剩余的堆继续调整为最大堆，再次将堆顶的最大数取出，这个过程持续到剩余数只有一个时结束。在堆中定义以下几种操作

• 最大堆调整（Max-Heapify）：将堆的末端子节点作调整，使得子节点永远小于父节点

• 创建最大堆（Build-Max-Heap）：将堆所有数据重新排序，使其成为最大堆
  

• 移除位在第一个数据的根节点，并做最大堆调整的递归运算
  

算法实现

需要注意的一个问题是：数组都是 Zero-Based，这就意味着我们的堆数据结构模型要发生改变即
对于给定下标为i的数组中的数组,其该元素所对应的父节点、孩子节点下标为(以0作为开始)：
父节点： Parent(i) = floor((i-1)/2)
左孩子节点： Left(i) = 2*i+1
右孩子节点: Right(i)= 2*(i+1)

对于利用堆排序，只关心两个问题

1. 给定一个无序数组，如何建立堆
2. 删除堆顶元素，如何调整成为新的堆

void heapSort(int arr[],int len){
    int lastIndex = len-1;
    //初始化最大堆
    //从第一个非叶子节点开始
    for(int i = getParentIndex(lastIndex); i>=0;i--)
        adjustHeap(arr,i,lastIndex);

    //删除堆顶元素,重新调整堆
    while(lastIndex>=0){
        swap(arr[0],arr[lastIndex]);
        lastIndex--;
        adjustHeap(arr,0,lastIndex);
    }
}

void adjustHeap(int arr[], int curIndex, int endIndex){
    int left,right,exchangeIndex;
    left = getLeftChildIndex(curIndex);
    while(left <= endIndex){
        //选择左右孩子中较大的进行交换
        right = left  + 1;
        exchangeIndex = left;
        if(right <= endIndex && arr[left] < arr[right]){
            exchangeIndex = right;
        }
        //若当前节点小于其孩子节点，交换并下沉
        if(arr[curIndex] < arr[exchangeIndex]){
            swap(arr[curIndex],arr[exchangeIndex]);
            curIndex = exchangeIndex;
            left = getLeftChildIndex(curIndex);
        }else{
            break;
        }
    }
}
int getParentIndex(int index){
    return (index-1) /2;
    }
int getLeftChildIndex(int index){
    return 2 * index + 1;
}

算法特点

1. 堆排序存在大量的筛选和移动过程，属于不稳定的排序算法
2. 堆排序在建立堆和调整堆的过程中会产生比较大的开销，在元素少的时候并不适用
3. 在元素比较多的情况下,尤其是在解决诸如“前n大的数”一类问题时，几乎是首选算法。

计数排序

计数排序不是基于比较的排序算法，其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。

算法描述

1. 找出待排序的数组中最大和最小的元素；
2. 统计数组中每个值为i的元素出现的次数，存入数组C的第i项；
3. 对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）；
4. 反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1

动图演示

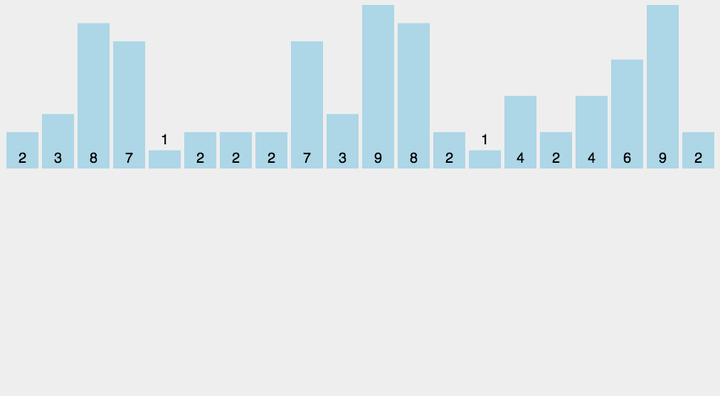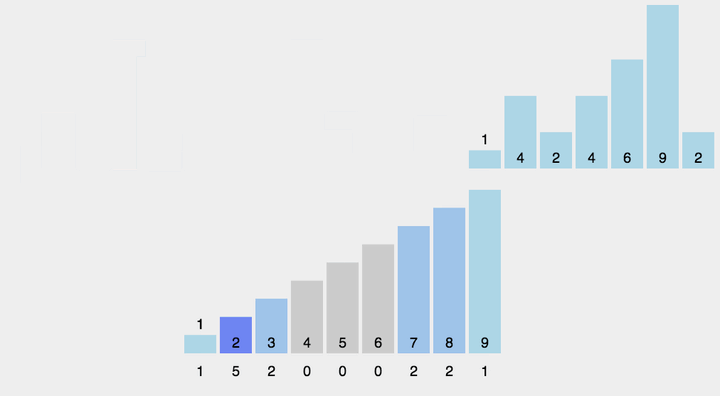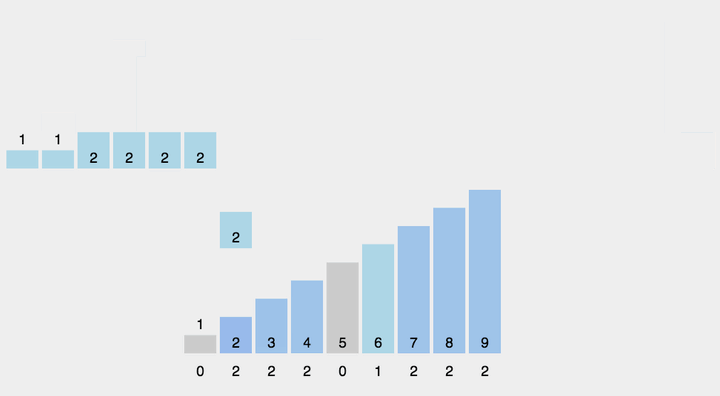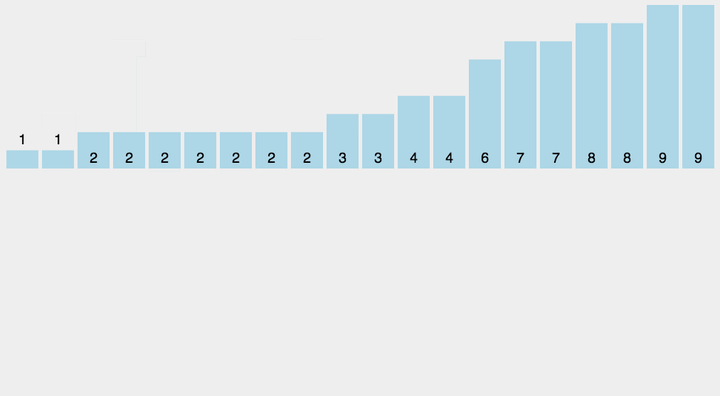
算法实现

void countSort(int arr[],int len, int maxVal, int minVal){
    int cntLen = maxVal- minVal + 1;
    int* cntVec = new int[cntLen];
    //初始化为0
    for(int i = minVal; i <= maxVal;i++)
        cntVec[i] = 0;

    //统计每个值出现的次数
    for(int i = 0; i < len; i++ ){
        cntVec[arr[i]-minVal]++;
    }

    //按照计数顺序将其依次填充到原数组中
    int p = 0;  //指向计数数组
    int curIndex = 0; //指向需要被填充的数组
    while(p < cntLen){
        while(cntVec[p] > 0){
            arr[curIndex++] = p + minVal;
            cntVec[p]--;
        }
        p++;
    }
    delete []cntVec;

}

算法特点

1. 排序目标要能够映射到整数域，其最大值最小值应当容易辨别
2. 计数排序需要占用大量空间，它比较适用于数据比较集中的情况

桶排序

桶排序又叫箱排序，是计数排序的升级版，它的工作原理是将数组分到有限数量的桶子里，然后对每个桶子再分别排序（有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排序），最后将各个桶中的数据有序的合并起来。

计数排序是桶排序的一种特殊情况，可以把计数排序当成每个桶里只有一个元素的情况
桶排序是计数排序的升级版。它利用了函数的映射关系，高效与否的关键就在于这个映射函数的确定。为了使桶排序更加高效，我们需要做到这两点：

1. 在额外空间充足的情况下，尽量增大桶的数量
2. 使用的映射函数能够将输入的 N 个数据均匀的分配到 K 个桶中

算法描述

1. 找出待排序数组中的最大值max、最小值min
2. 使用数组作为桶，桶里放的元素用存储。桶的数量为(max-min)/arr.length+1
3. 遍历数组 arr，计算每个元素 arr[i] 放的桶
4. 每个桶各自排序
5. 遍历桶数组，把排序好的元素放进输出数组

图片解释

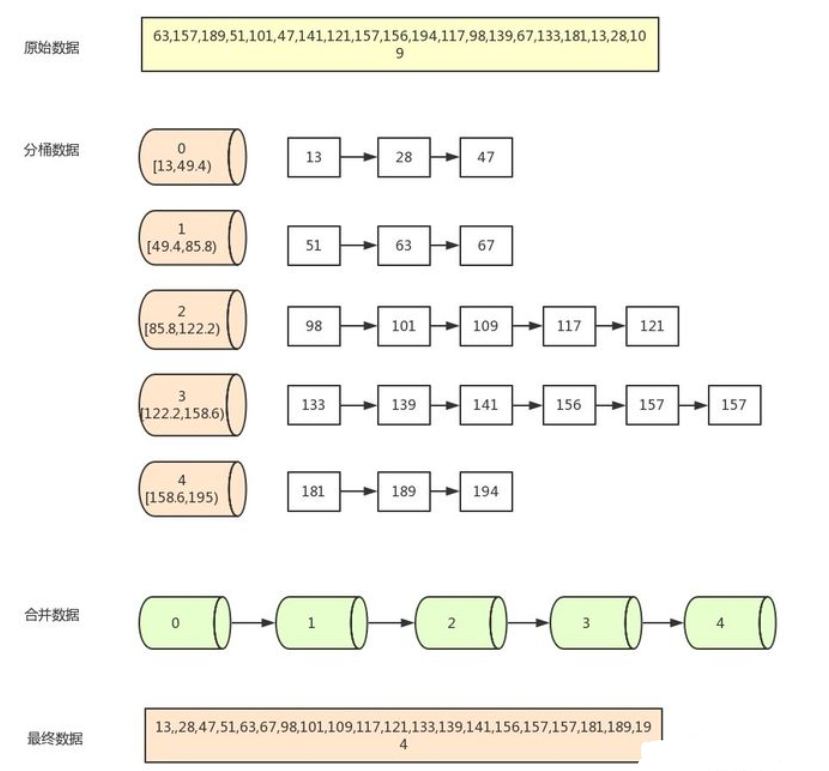
算法特点

1. 当输入数据可以均匀的分配到桶最快
2. 空间复杂度：O(n+k)，时间复杂度O(n+k)

基数排序

基数排序(Radix Sort)是桶排序的扩展，它的基本思想是：将整数按位数切割成不同的数字，然后按每个位数分别比较。
排序过程：将所有待比较数值（正整数）统一为同样的数位长度，数位较短的数前面补零。然后，从最低位开始，依次进行一次排序。这样从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列。

实际上，基数排序算法对排序元素的类型不要求一定是非负整数才可以进行，其对于字符串、浮点数等类型均可适用。其关键在于要求排序元素的数位长度统一。例如对整数排序时，如果排序元素中含有负数，则可以对排序元素均加上一个数使其全部为非负整数；如果元素类型是字符串的话，在计数排序过程中，可以直接使用该位字符对应ASCII码值进行计数，对于长度不足的字符串，可直接在其后面补0实现长度对齐。即在计数排序过程中，如果发现某位字符是为对齐所填充的0的话，则可认为其对应的ASCII码值为0进行计数，因为字符’A’所对应的ASCII码值是65，字符’0’所对应的ASCII码值是48，均比0大。这样即可保证基数排序的结果是符合字典序的实现

动图演示

算法特点

1. 通过上面的排序过程，我们可以看到，每一轮映射和收集操作，都保持从左到右的顺序进行，如果出现相同的元素，则保持他们在原始数组中的顺序。可见，基数排序是一种稳定的排序。

2. 基数排序要求较高，元素必须是整数，整数时长度10W以上，最大值100W以下效率较好，但是基数排序比其他排序好在可以适用字符串，或者其他需要根据多个条件进行排序的场景，例如日期，先排序日，再排序月，最后排序年 ，其它排序算法可是做不了的