排序算法(一)——冒泡、选择、插入

排序算法是最基本的算法。排序算法分为内部排序和外部排序。

内部排序：数据记录在内存中进行排序，不需要访问外存

外部排序：因排序的数据很大，一次不能容纳全部的排序记录，在排序过程中需要访问外存。

常见的内部排序算法有：插入排序、希尔排序、选择排序、冒泡排序、归并排序、快速排序、堆排序、基数排序等。用一张图概括：

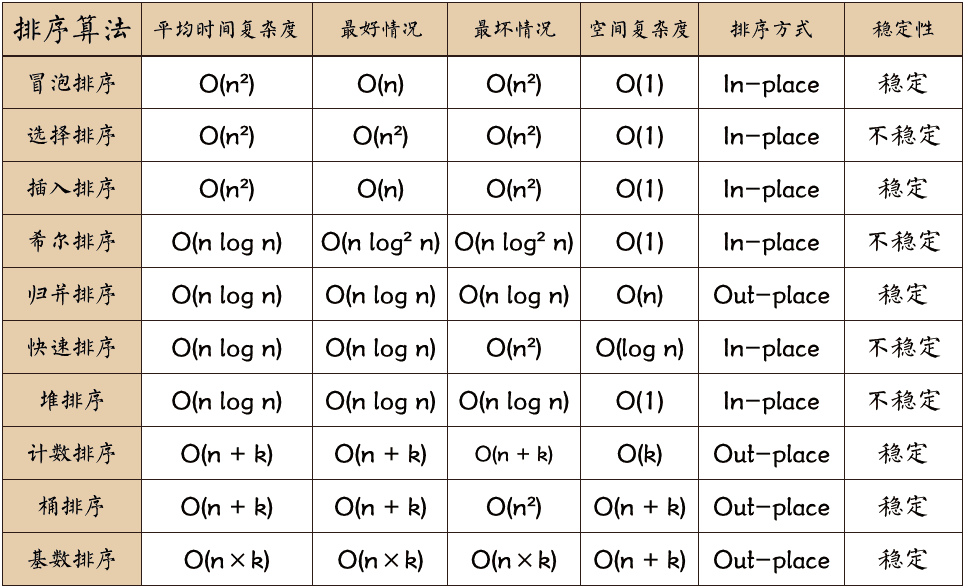
名词解释:

• n 数据规模
• k 桶的个数
• In-place 占用常数内存，不占用额外内存
• Out-place 占用额外内存
• 稳定性 排序后 2 个相等键值的顺序和排序之前它们的顺序相同

冒泡排序

冒泡排序（Bubble Sort）是一种简单直观的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢"浮"到数列的顶端。

算法描述

1. 比较相邻元素，如果第一个比第二个大，则交换他们的位置
2. 对每一对相邻元素对同样的工作，从开始第一对到结尾的最后一对，
3. 针对所有元素重复以上的步骤，除了最后一个
4. 重复步骤1～3,知道所有排序完成

动图演示

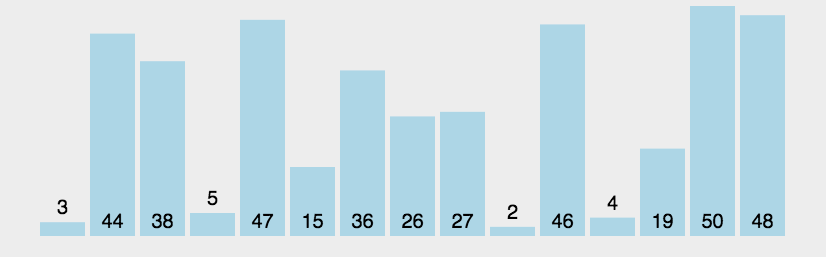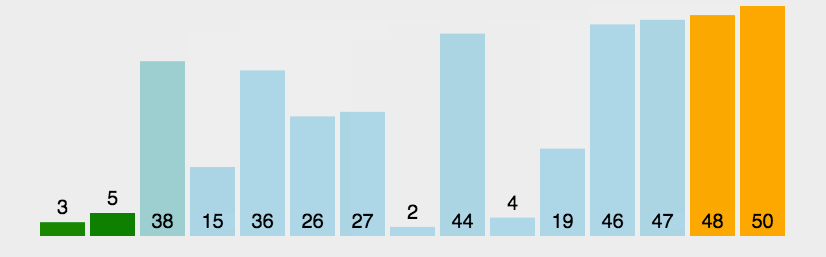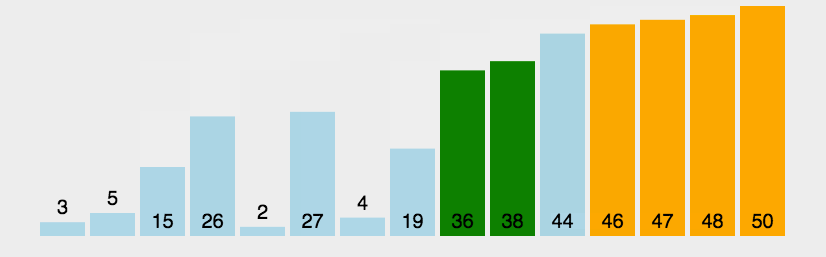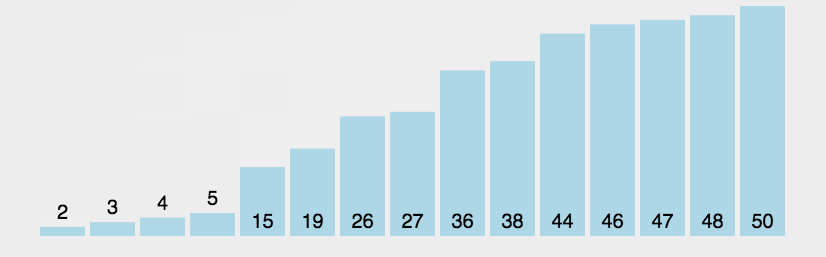
算法实现

void bubbleSort(int arr[],int len){
    for(int i = len-1;i>0;i--){// 需要排序的长度，共len-1次循环
        for(int j = 0;j<i;j++){//从第1个元素到第i个元素
          if(arr[j]>arr[j+1])
              swap(arr[j],arr[j+1]);
        }//end loop j
    }//end loop i
}

算法特点

1. 在相邻元素相等时，它们并不会交换位置，所以，冒泡排序是稳定排序
2. 每完成一次第一层循环，会使得当前需要排序的数组 arr[0]-arr[i]中最大的数被放置末尾下标为i的位置
3. 算法复杂度总是O(n^2)，除非有序状态下提前结束，也需要O(n)
4. 冒泡排序思路简单，代码也简单，特别适合小数据的排序。但是，由于算法复杂度较高，在数据量大的时候不适合使用。

代码优化

要使算法在最佳情况下有O(n)复杂度，需要做一些改进，增加一个swap的标志，当前一轮没有进行交换时，说明数组已经有序，没有必要再进行下一轮的循环了，直接退出。(意义不大)

void bubbleSort(int arr[],int len){
    bool isSwap = false;
    for(int i = len-1;i>0;i--){// 需要排序的长度，共len-1次循环
        for(int j = 0;j<i;j++){//从第1个元素到第i个元素
            if(arr[j]>arr[j+1]){
              swap(arr[j],arr[j+1]);
              isSwap = true;
            }        	
        }//end loop j
      //没有交换，提前结束
      if(!isSwap){
        break;
      }
    }//end loop i
}

选择排序

选择排序是一种简单直观的排序算法，它也是一种交换排序算法，和冒泡排序有一定的相似度，可以认为选择排序是冒泡排序的一种改进。

算法描述

1. 在未排序序列中找到最小（大）元素，存放到排序序列的起始位置
2. 从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾
3. 重复第二步，直到所有元素均排序完毕

动图演示

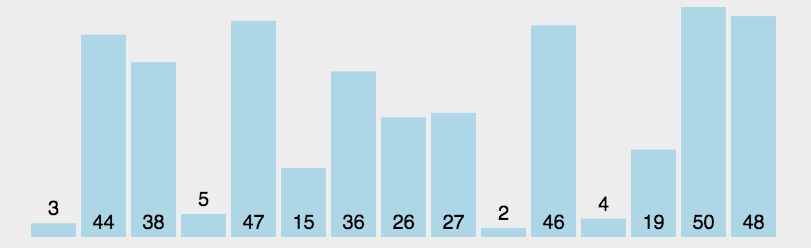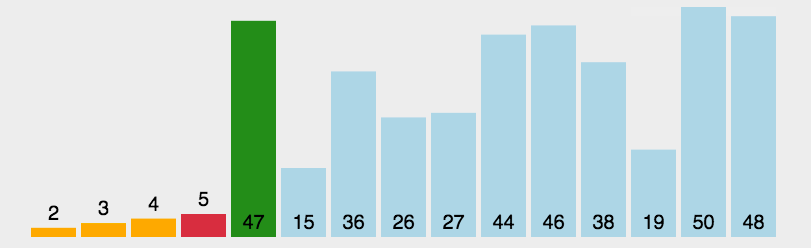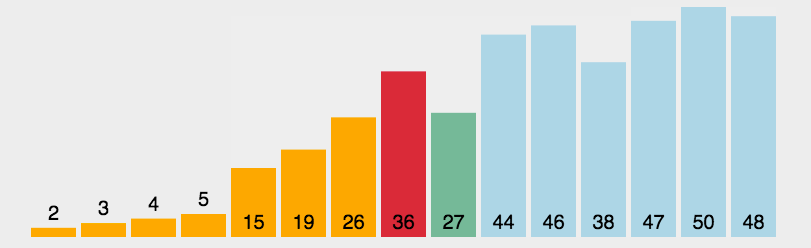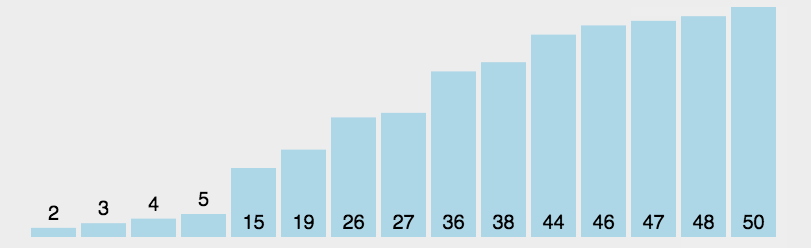
算法实现

void selectionSort(int arr[],int len){
    int minIndex;
    //有序序列 [0,i)
    //无序序列 [i,len)
    for(int i = 0; i<len-1;i++){
        minIndex = i;
        //寻找无序序列中中最小的元素
        for(int j =i;j<len;j++)
            if(arr[j] < arr[min]){
              	minIndex = j;
            }      	
      //将最小值与无序序列第一个值交换
      	swap(arr[minIndex],arr[i]);
    }
}

算法特点

1. 选择排序实现也比较简单，并且由于在各种情况下复杂度波动小，因此一般是优于冒泡排序的
2. 数组实现的选择排序是不稳定的，用链表实现的选择排序是稳定的
3. 算法复杂度总是O(n^2)

插入排序

插入排序是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入

算法描述

1. 把待排序的数组分成已排序和未排序两部分，初始的时候把第一个元素认为是已排好序的
2. 从第二个元素开始，在已排好序的子数组中寻找到该元素合适的位置并插入该位置
3. 重复上述过程直到最后一个元素被插入有序子数组中

动图演示

算法实现

void insertionSort(int arr[],int len){
    //有序序列 [0,i）
    //无序序列 [i,len)
    for(int i = 1; i < len; i++){
        //需要插入的值
        int curVal = arr[i];

        //寻找可以插入的位置
        int pos = i;
        //逐个比较，若arr[pos-1]大于插入的值则向后移动
        while(pos >=1 && arr[pos-1]>curVal){
            arr[pos] = arr[pos-1];
            pos--;
        }
        arr[pos] = curVal;
    }
}

算法特点

1. 由于只需要找到不大于当前数的位置而并不需要交换，因此，直接插入排序是稳定的排序方法
2. 算法复杂度总是O(n^2),在数据比较少的时候，是一个不错的选择，一般做为快速排序的扩充